|
|||||

|

|
|

|

|
|
Descent for
differential Galois theory of difference equations:
confluence and q-dependence
Lucia Di Vizio and Charlotte Hardouin |
|
Vol. 256 (2012), No. 1, 79–104
|
Abstract |
|
The present paper
contains two results that generalize and improve constructions of Hardouin and
Singer. In the case of a derivation, we prove that the parametrized Galois
theory for difference equations constructed by Hardouin and Singer can be
descended from a differentially closed to an algebraically closed field. In
the second part of the paper, we show that the theory can be applied to
deformations of q-series to study the differential dependence with respect
to x |
Keywords
linear difference equations, Galois theory,
hypertranscendence
|
Mathematical Subject Classification 2010
Primary: 12H99, 39A13, 39A99
|
Milestones
Received: 25 March 2011
Revised: 25 November 2011
Accepted: 29 November 2011
Published: 6 May 2012
|
Authors |
| Lucia Di Vizio | |
| Laboratoire de Mathématiques,
bâtiment Fermat Université de Versailles-St Quentin 45 avenue des États-Unis 78035 Versailles Cedex France |
|
| http://divizio.perso.math.cnrs.fr/ | |
| Charlotte Hardouin | |
| Institut de Mathématiques de
Toulouse Université Paul Sabatier 118 route de Narbonne 31062 Toulouse Cedex 9 France |
|
| http://www.math.univ-toulouse.fr/~hardouin/ | |
 |
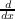 and
and 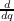 . We show that the parametrized difference Galois group
(with respect to a convenient derivation defined in the text) of the Jacobi
Theta function can be considered as the Galoisian counterpart of the heat
equation.
. We show that the parametrized difference Galois group
(with respect to a convenient derivation defined in the text) of the Jacobi
Theta function can be considered as the Galoisian counterpart of the heat
equation.