Energy identity and removable singularities of maps from a Riemann surface with tension field unbounded in L²

Yong Luo

Vol. 256 (2012), No. 2, 365–380

DOI: 10.2140/pjm.2012.256.365

Abstract

We prove removable singularity results for maps with bounded energy from the unit disk B of ℝ² centered at the origin to a closed Riemannian manifold whose tension field is unbounded in L²(B) but satisfies the following condition: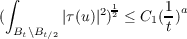

for some 0 < a < 1 and any 0 < t < 1, where C₁ is a constant independent of t.

We will also prove that if a sequence {u_n} has uniformly bounded energy and satisfies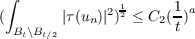

for some 0 < a < 1 and any 0 < t < 1, where C₂ is a constant independent of n and t, then the energy identity holds for this sequence and there will be no neck formation during the blow up process.

Keywords

harmonic maps, energy identity

Mathematical Subject Classification 2010

Primary: 35B44

Milestones

Received: 16 February 2011

Revised: 2 December 2011

Accepted: 27 February 2012

Published: 30 May 2012