|
|||||

|

|
|

|

|
|
On orthogonal
polynomials with respect to certain discrete Sobolev inner
product
Francisco Marcellán, Ramadan Zejnullahu, Bujar Fejzullahu and Edmundo Huertas |
|
Vol. 257 (2012), No. 1, 167–188
|
Abstract |
|
In this paper we deal with sequences of polynomials orthogonal with respect to the discrete Sobolev inner product 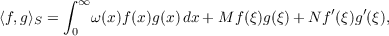 where ω is a weight function, ξ ≤ 0, and M,N ≥ 0. The location of the zeros of discrete Sobolev orthogonal polynomials is given in terms of the zeros of standard polynomials orthogonal with respect to the weight function ω. In particular, for ω(x) = xαe−x we obtain the asymptotics for discrete Laguerre–Sobolev orthogonal polynomials. |
Keywords
orthogonal polynomials, discrete Sobolev polynomials,
Laguerre polynomials, asymptotics
|
Mathematical Subject Classification 2010
Primary: 33C47
Secondary: 42C05
|
Milestones
Received: 20 June 2011
Revised: 23 January 2012
Accepted: 25 January 2012
Published: 19 June 2012
|
Authors |
| Francisco Marcellán | |
| Departamento de Matemáticas Escuela Politécnica Superior Universidad Carlos III de Madrid Avenida de la Universidad 30 28911 Leganés Spain |
|
| Ramadan Zejnullahu | |
| Faculty of Mathematics and
Sciences University of Prishtina Mother Teresa 5 10000 Prishtina Kosovo |
|
| Bujar Fejzullahu | |
| Faculty of Mathematics and
Sciences University of Prishtina Mother Teresa 5 1000 Prishtina Kosovo |
|
| Edmundo Huertas | |
| Departamento de Matematicas Escuela Politécnica Superior Universidad Carlos III de Madrid Avenida de la Universidad 30 28911 Leganés Spain |
|
 |
