|
|||||

|

|
|

|

|
|
On a conjecture of
Kaneko and Ohno
Zhong-hua Li |
|
Vol. 257 (2012), No. 2, 419–430
|
Abstract |
|
Let X0⋆(k,n,s) denote the sum of all multiple zeta-star values of weight k, depth n and height s. Kaneko and Ohno conjectured that, for any positive integers m,n,s with m,n ≥ s, the difference 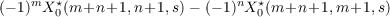 can be expressed as a polynomial of zeta values with rational coefficients. We give a proof of this conjecture. |
Keywords
multiple zeta-star values, generalized hypergeometric
function
|
Mathematical Subject Classification 2010
Primary: 11M32, 33C20
|
Milestones
Received: 27 June 2011
Accepted: 4 June 2012
Published: 4 July 2012
|
Authors |
| Zhong-hua Li | |
| Department of Mathematics Tongji University No. 1239 Siping Road Shanghai 200092 China |
Graduate School of Mathematical
Sciences The University of Tokyo 3-8-1 Komaba, Meguro Tokyo 153-8914 Japan |
 |
