|
|||||

|

|
|

|

|
|
Comparing seminorms
on homology
Jean-François Lafont and Christophe Pittet |
|
Vol. 259 (2012), No. 2, 373–385
|
Abstract |
|
We compare the l1-seminorm ∥⋅∥1 and the manifold seminorm ∥⋅∥man on n-dimensional integral homology classes. Crowley and Löh showed that for any topological space X and any α ∈ Hn(X; ℤ), with n≠3, the equality ∥α∥man = ∥α∥1 holds. We compute the simplicial volume of the 3-dimensional Tomei manifold and apply Gaifullin’s desingularization to establish the existence of a constant δ3 ≈ 0.0115416, with the property that for any X and any α ∈ H3(X; ℤ), one has the inequality 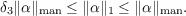 |
Keywords
l1-norm, simplicial volume, singular
homology, manifold norm, Steenrod’s realization problem,
Thurston norm, Tomei manifold
|
Mathematical Subject Classification 2010
Primary: 53C23
Secondary: 57M50
|
Milestones
Received: 28 March 2012
Revised: 2 August 2012
Accepted: 21 August 2012
Published: 3 October 2012
|
Authors |
| Jean-François Lafont | |
| Department of Mathematics The Ohio State University 100 Math Tower 231 West 18th Avenue Columbus, Ohio 43210-1174 United States |
|
| Christophe Pittet | |
| Centre de Mathématiques et
Informatique Aix-Marseille Université 39 rue Frédéric Joliot-Curie 13453 Marseille Cedex 13 France |
|
 |
