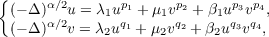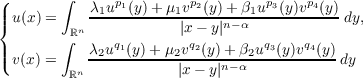|
|||||

|

|
|

|

|
|
Classification of
positive solutions for an elliptic system with a higher-order
fractional Laplacian
Jingbo Dou and Changzheng Qu |
|
Vol. 261 (2013), No. 2, 311–334
|
Abstract |
||
|
We discuss properties of solutions to the following elliptic PDE system in ℝn:
where 0 < α < n, λj, μj,βj (j = 1,2) are nonnegative constants and pi and qi (i = 1,2,3,4) satisfy some suitable assumptions. It is shown that this PDE system is equivalent to the integral system
in ℝn. The radial symmetry, monotonicity and regularity of positive solutions are proved via the method of moving plane in integral forms and a regularity lifting lemma. For the special case with 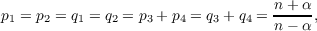 positive solutions of the integral system (or the PDE system) are classified. Furthermore, our symmetry results, together with some known results on nonexistence of positive solutions, imply that, under certain integrability conditions, the PDE system has no positive solution in the subcritical case. |
Keywords
system of integral equations, regularity, moving plane
method in integral form, classification of solutions
|
Mathematical Subject Classification 2010
Primary: 35J99, 45K05, 35R09, 35J48, 35B65, 45G15
|
Milestones
Received: 22 July 2011
Revised: 7 September 2012
Accepted: 26 December 2012
Published: 20 March 2013
|
Authors |
| Jingbo Dou | |
| School of Statistics Xi’an University of Finance and Economics 710100 Xi’an China |
|
| Changzheng Qu | |
| Center for Nonlinear Studies Ningbo University 315211 Ningbo China |
|
 |