On the finite generation of a family of Ext modules

Tony J. Puthenpurakal

Vol. 266 (2013), No. 2, 367–389

DOI: 10.2140/pjm.2013.266.367

Abstract

Let (A,m) be a local complete intersection ring. Let M,N be finitely generated A-modules and let I be an ideal in A. We show that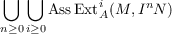

is a finite set. We also show that there exist i₀,n₀ such that for all i ≥ i₀ and n ≥ n₀ we have

We prove analogous results for complete intersection rings which arise in algebraic geometry. We also prove that the complexity, cx(M,IⁿN), is constant for all n ≫ 0.

Keywords

local complete intersection, asymptotic associate primes, cohomological operators

Mathematical Subject Classification 2010

Primary: 13D07, 13H10

Secondary: 13A15, 13A02

Milestones

Received: 18 September 2008

Revised: 11 April 2013

Accepted: 11 September 2013

Published: 12 November 2013